Trigonometry and prosthaphaeresis rules

A ready-to-use set of trigonometry and prosthaphaeresis rules

trigonometry

prosthaphaeresis

Geometrical Definitions

Unitary circle and trigonometric functions definition

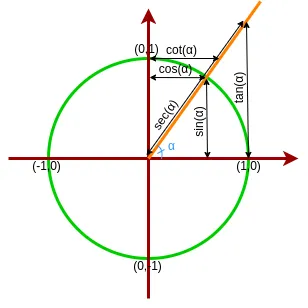
Trigonometric functions are fundamental mathematical functions that relate the angles of a triangle to the lengths of its sides. These functions are essential when studying periodic phenomena, wave patterns, and oscillations, and they have extensive applications in fields such as physics, engineering, astronomy, and computer science.

Trigonometric functions can also be defined using the unit circle, a circle with a radius of 1, centred at the origin of the coordinate plane. Take a look at the image aside.

Understanding trigonometric functions is crucial for solving problems involving angles and distances, modelling periodic behaviours, and analyzing waves and harmonic motion.

Triangle relations

Right triangle with angles and sides named

Trigonometric functions can be used to find the sizes of a right triangle using the measure of the angles. The relations are shown below: $$sin(\alpha)=\frac{c}{a} \qquad csc(\alpha)=\frac{a}{c}$$ $$cos(\alpha)=\frac{b}{a} \qquad sec(\alpha)=\frac{a}{b}$$ $$tan(\alpha)=\frac{c}{b} \qquad cot(\alpha)=\frac{b}{c}$$

Trigonometry Rules Table

Definitions

$$tan(x)=\frac{sin(x)}{cos(x)}$$		$$cot(x)=\frac{cos(x)}{sin(x)}$$
$$csc(x)=\frac{1}{sin(x)}$$		$$sec(x)=\frac{1}{cos(x)}$$
$$sin(x)=\frac{1}{csc(x)}$$		$$cos(x)=\frac{1}{sec(x)}$$
$$tan(x)=\frac{1}{cot(x)}$$		$$cot(x)=\frac{1}{tan(x)}$$

Pythagorean Identities

$$sin^2(x)+cos^2(x) = 1$$

$$tan^2(x)+1 = sec^2(x)$$

$$cot^2(x)+1 = csc^2(x)$$

Equivalence Rules

$$sin(x+2\pi n) = sin(x)$$	$$cos(x+2\pi n) = cos(x)$$	$$tan(x+\pi n) = tan(x)$$
$$csc(x+2\pi n) = csc(x)$$	$$sec(x+2\pi n) = sec(x)$$	$$cot(x+\pi n) = cot(x)$$
$$sin(-x) = -sin(x)$$	$$cos(-x) = cos(x)$$	$$tan(-x) = -tan(x)$$
$$csc(-x) = -csc(x)$$	$$sec(-x) = sec(x)$$	$$cot(-x) = -cot(x)$$

Sum-Subtraction rules table

$$sin(x+y) = sin(x)cos(y)+cos(x)sin(y)$$	$$sin(x-y) = sin(x)cos(y)-cos(x)sin(y)$$
$$cos(x+y) = cos(x)cos(y)-sin(x)sin(y)$$	$$cos(x-y) = cos(x)cos(y)+sin(x)sin(y)$$
$$tan(x+y) = \frac{tan(x)+tan(y)}{1-tan(x)tan(y)}$$	$$tan(x-y) = \frac{tan(x)-tan(y)}{1+tan(x)tan(y)}$$

Half/Double angle identities

$$sin(2x) = 2sin(x)cos(x)$$	$$cos(2x) = cos^2(x)-sin^2(x)$$	$$tan(2x) = \frac{2tan(x)}{1-tan^2(x)}$$
$$sin(\frac{x}{2}) = \pm \sqrt{\frac{1-cos(x)}{2}}$$	$$cos(\frac{x}{2}) = \pm \sqrt{\frac{1+cos(x)}{2}}$$	$$tan(\frac{x}{2}) = \pm \sqrt{\frac{1-cos(x)}{1+cos(x)}}$$

Prosthaphaeresis rules table

$$sin(x)sin(y) = \frac{1}{2}(cos(x-y)-cos(x+y))$$	$$cos(x)cos(y) = \frac{1}{2}(cos(x-y)+cos(x+y))$$
$$sin(x)cos(y) = \frac{1}{2}(sin(x+y)+sin(x-y))$$	$$cos(x)sin(y) = \frac{1}{2}(sin(x+y)-sin(x-y))$$
$$sin(x) + sin(y) = 2sin\frac{x+y}{2}cos\frac{x-y}{2}$$	$$sin(x) - sin(y) = 2cos\frac{x+y}{2}sin\frac{x-y}{2}$$
$$cos(x) + cos(y) = 2cos\frac{x+y}{2}cos\frac{x-y}{2}$$	$$cos(x) - cos(y) = -2sin\frac{x+y}{2}sin\frac{x-y}{2}$$

Notables Values

$$sin(n\pi) = 0$$	$$sin(\frac{\pi}{6}) = \frac{1}{2}$$	$$sin(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$$	$$sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}$$	$$sin(\frac{\pi}{2}) = 1$$
$$cos(n\pi) = 1$$	$$cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2}$$	$$cos(\frac{\pi}{4}) = \frac{\sqrt{2}}{2}$$	$$cos(\frac{\pi}{3}) = \frac{1}{2}$$	$$cos(\frac{\pi}{2}) = 0$$
$$tan(n\pi) = 0$$	$$tan(\frac{\pi}{6}) = \frac{\sqrt{3}}{3}$$	$$tan(\frac{\pi}{4}) = 1$$	$$tan(\frac{\pi}{3}) = \sqrt{3}$$	$$tan(\frac{\pi}{2}) = \infty$$
$$cot(n\pi) = \infty$$	$$cot(\frac{\pi}{6}) = \sqrt{3}$$	$$cot(\frac{\pi}{4}) = 1$$	$$cot(\frac{\pi}{3}) = \frac{\sqrt{3}}{3}$$	$$cot(\frac{\pi}{2}) = 0$$
$$sec(n\pi) = 1$$	$$sec(\frac{\pi}{6}) = \frac{2\sqrt{3}}{3}$$	$$sec(\frac{\pi}{4}) = \sqrt{2}$$	$$sec(\frac{\pi}{3}) = 2$$	$$sec(\frac{\pi}{2}) = \infty$$
$$csc(n\pi) = \infty$$	$$csc(\frac{\pi}{6}) = 2$$	$$csc(\frac{\pi}{4}) = \sqrt{2}$$	$$csc(\frac{\pi}{3}) = \frac{2\sqrt{3}}{3}$$	$$csc(\frac{\pi}{2}) = 1$$