Integrals

A ready-to-use page about integrals rules, properties and notable cases

cheatsheet

integral

Key concepts

Different methods of a Riemann's integral

Integrals are fundamental mathematical tools used to compute the accumulation of quantities over a given interval or area under a curve. At its core, integration involves breaking down a complex shape or function into infinitesimally small pieces, summing them together, and then taking the limit as the size of these pieces approaches zero. This process allows us to find the total area under a curve, the total volume of a solid shape, or other accumulated quantities.

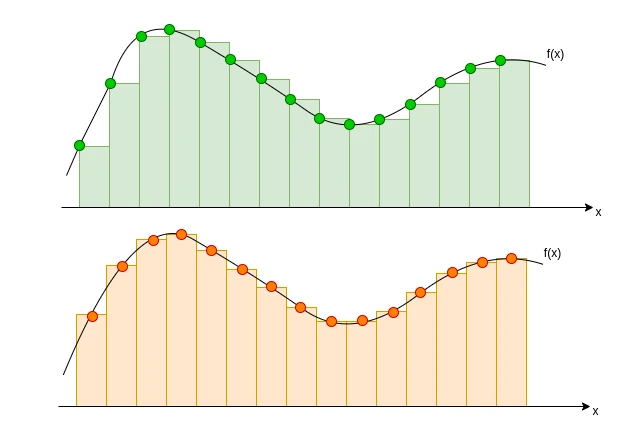
The simplest integration method is the so-called Riemann's integral: it was developed by Bernhard Riemann in the mid-19th century and is the classical notion of integration taught in most calculus courses. It defines the integral of a function as the limit of a sum of function values multiplied by the width of equally spaced intervals, as the width of the intervals approaches zero. This method works well for integrating continuous functions on closed intervals and is conceptually straightforward. $$\int_a^b f(x) dx \Rightarrow \lim_{n\rightarrow \infty}{\sum_{i=0}^n f(x_i) \Delta_i}$$ where $$a \leq x_0 \leq x_1 \leq x_2 \leq x_3 \leq ... \leq x_n \leq b, \quad \Delta_i = x_1-x_0 = x_2-x_1 = ... = x_n-x_{n-1}$$ Different results can be obtained according to the point chosen to evaluate the function, as shown in the image. However, by increasing the number of intervals (reducing thus Δ_i) all the methods will converge to the exact result.

Fundamental theorem of calculus

The fundamental theorem of calculus connects differentiation and integration, stating that differentiation and integration are inverse processes. Specifically, it asserts that if f is defined and continuous in the interval [a,b], then there exists a function F(x) such that: $$F(x) = \int_a^x f(t) dt$$ F(x) is continuous in [a,b] and differentiable in (a,b) and the following law, in the (a,b) range, will always be true: $$F'(x) = f(x)$$

Integration rules and integral properties

Expression		Equivalent	Expression		Equivalent
$$\int (f(t)+ g(t)) \ dt$$	$$\Rightarrow$$	$$\int f(t) \ dt+ \int g(t) \ dt$$	$$\int a f(t) \ dt, \ a \ \in \mathbb{R}$$	$$\Rightarrow$$	$$a\int f(t) \ dt$$
$$\int \int f(t) \ dt^2$$	$$\Rightarrow$$	$$\int \left( \int f(t) \ dt\right) \ dt$$	$$\int f(t)g'(t) \ dt$$	$$\Rightarrow$$	$$f(t)g(t) - \int f'(t) g(t) \ dt$$
$$\int_a^b f(t) \ dt$$	$$\Rightarrow$$	$$\int_a^c f(t) \ dt + \int_c^b f(t) \ dt, \ a \lt c \lt b$$	$$\int_a^b f(t) \ dt$$	$$\Rightarrow$$	$$-\int_b^a f(t) \ dt$$

Notable cases

Expression		Equivalent	Expression		Equivalent
$$\int a \ dt, \ a \ \in \mathbb{R}$$	$$\Rightarrow$$	$$at + C$$	$$\int at \ dt, \ a \ \in \mathbb{R}$$	$$\Rightarrow$$	$$a\frac{t^2}{2} + C$$
$$\int at^n \ dt, \ a \ \in \mathbb{R}$$	$$\Rightarrow$$	$$a\frac{t^{n+1}}{n+1} + C$$	$$\int \frac{1}{t} \ dt$$	$$\Rightarrow$$	$$ln\|t\| + C$$
$$\int be^{at} \ dt, \ a,b \ \in \mathbb{R}$$	$$\Rightarrow$$	$$\frac{b}{a}e^{at} + C$$	$$\int bc^{at} \ dt, \ a,b \ \in \mathbb{R}$$	$$\Rightarrow$$	$$\frac{b}{aln(c)}c^{at} + C$$
$$\int f'(t)e^{f(t)} \ dt$$	$$\Rightarrow$$	$$e^{f(t)} + C$$	$$\int (f'(t)+f(t))e^{t} \ dt$$	$$\Rightarrow$$	$$f(t)e^t + C$$
$$\int ln(t) \ dt$$	$$\Rightarrow$$	$$tln(t)-t + C$$	$$\int log_a(t) \ dt$$	$$\Rightarrow$$	$$tlog_a(t)-\frac{t}{ln(a)} + C$$
$$\int sin(2\pi ft) \ dt$$	$$\Rightarrow$$	$$\frac{-cos(2\pi ft)}{2\pi f} + C$$	$$\int cos(2\pi ft) \ dt$$	$$\Rightarrow$$	$$\frac{sin(2\pi ft)}{2\pi f} + C$$
$$\int tan(2\pi ft) \ dt$$	$$\Rightarrow$$	$$\frac{-ln\|cos(2\pi ft)\|}{2\pi f} + C$$	$$\int cot(2\pi ft) \ dt$$	$$\Rightarrow$$	$$\frac{ln\|sin(2\pi ft)\|}{2\pi f} + C$$