Electricity
A ready-to-use cheat sheet with methods and formulas to solve electrical circuit
Definitions
| Symbol | Name | Expression | Unit |
|---|---|---|---|
| $$Z$$ | Impedance | $$Z=R+jX=Y^{-1}$$ | $$\left[ Ohm \right]$$ |
| $$R$$ | Resistance | $$G^{-1} \quad if \quad X=0$$ | $$\left[ Ohm \right]$$ |
| $$X$$ | Reactance | $$B^{-1} \quad if \quad R=0$$ | $$\left[ Ohm \right]$$ |
| $$Y$$ | Admittance | $$Y=G+jB=Z^{-1}$$ | $$\left[ S \right]$$ |
| $$G$$ | Conductance | $$R^{-1} \quad if \quad B=0$$ | $$\left[ S \right]$$ |
| $$B$$ | Susceptance | $$X^{-1} \quad if \quad G=0$$ | $$\left[ S \right]$$ |
| $$S$$ | Complex power | $$S=P+jQ$$ | $$\left[ VA \right]$$ |
| $$P$$ | Active power | $$-$$ | $$\left[ W \right]$$ |
| $$Q$$ | Reactive power | $$-$$ | $$\left[ VAR \right]$$ |
Ohm's laws
First Ohm's law
$$V = I \cdot Z$$ $$I = V \cdot Y$$
Second Ohm's law
$$R=\rho \frac{l}{A}, \quad \rho \ in \ Ohm \cdot m$$
Combination of impedances
Series
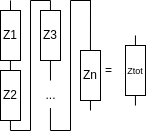
$$Z_{tot} = Z_1 + Z_2 + Z_3 + ... + Z_n = \sum_{i=1}^n R_i + j\sum_{i=1}^n X_i$$ $$R_{tot} = R_1 + R_2 + R_3 + ... + R_n = \sum_{i=1}^n R_i$$ $$X_{tot} = X_1 + X_2 + X_3 + ... + X_n = \sum_{i=1}^n X_i$$
Parallel
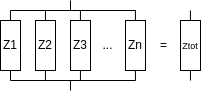
$$\frac{1}{Z_{tot}} = \frac{1}{Z_1} + \frac{1}{Z_2} + \frac{1}{Z_3} + ... + \frac{1}{Z_n}; \quad Z_{tot}=\frac{\prod_{i=1}^n Z_i}{\sum_{j=1}^n \left( \prod_{i=1,i\neq j}^n Z_i \right)}$$ $$if \ X=0 \quad \frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + ... + \frac{1}{R_n}; \quad R_{tot}=\frac{\prod_{i=1}^n R_i}{\sum_{j=1}^n \left( \prod_{i=1,i\neq j}^n R_i \right)}$$ $$if \ R=0 \quad \frac{1}{X_{tot}} = \frac{1}{X_1} + \frac{1}{X_2} + \frac{1}{X_3} + ... + \frac{1}{X_n}; \quad X_{tot}=\frac{\prod_{i=1}^n X_i}{\sum_{j=1}^n \left( \prod_{i=1,i\neq j}^n X_i \right)}$$
Kirchoff's laws
Kirchoff's junction law
$$I_1 + I_2 + I_3 + ... + I_n = 0 \quad \sum_{i=1}^n I_i = 0$$
Kirchoff's loop law
$$V_1 + V_2 + V_3 + ... + V_n = 0 \quad \sum_{i=1}^n V_i = 0$$
Voltage and current division
Voltage division
$$V_o = V_{tot} \frac{Z_1}{Z_1+Z_2}$$ $$V_o = V_{tot} \frac{Y_2}{Y_1+Y_2}$$
Current division
$$I_1 = I_{tot} \frac{Z_2}{Z_1+Z_2}$$ $$I_1 = I_{tot} \frac{Y_1}{Y_1+Y_2}$$
Millman's theorem
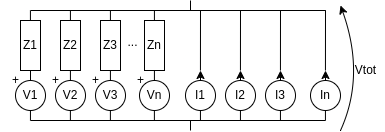
$$V_{tot} = \frac{\frac{V_1}{R_1} + \frac{V_2}{R_2}+ \frac{V_3}{R_3} +...+ \frac{V_n}{R_n} + I_1 + I_2 + I_3 +...+ I_m}{\frac{1}{R_1} + \frac{1}{R_2}+ \frac{1}{R_3} +...+ \frac{1}{R_l}} = \frac{\sum_{i=1}^n \frac{V_i}{R_i} + \sum_{i=1}^m I_i}{\sum_{i=1}^n \frac{1}{R_i}}$$
Power
DC power
Electric DC power is defined as $$P = V I$$ and measured in [W]. This formula represents the so-called active power, the amount of power actually consumed by the load that cannot be recovered in any way. With the passive sign convention, sources have negative and loads have positive power consumption.
For DC systems, the simplest linear and time-invariant load is the resistor; for this component, instantaneous active power and average active power have the same value. Power consumption is defined as: $$P = V I = I^2 R = \frac{V^2}{R} \qquad ; \qquad p(t) = v(t) i(t) = i^2(t) R = \frac{v^2(t)}{R}$$
If, instead, the load is purely reactive, there will be no active power consumption: $$P = V I = 0 \qquad ; \qquad p(t) = v(t) i(t) = 0$$ If the load is purely reactive and the applied voltage changes in time, power goes back and forth from source to load and vice versa (the average power is 0W but the instantaneous power changes in time). If the load is a capacitor, then the absorbed (but not lost!) power is $$p(t) = v(t) C\frac{dv(t)}{dt}$$ If, instead, the load is an inductor, the absorbed power (again, not lost, just transferred from the source to the load) is $$p(t) = L\frac{di(t)}{dt} i(t)$$
At steady state, in DC systems, only active power is absorbed, since all reactive components behave like open or short circuits. Some energy remains stored in those components and it will be dissipated when the system is turned off.
AC power
When dealing with AC systems (with sinusoidal voltages), power calculations become a little bit more complex and they cannot be limited to active power only. First of all, let's find a simple expression for the instantaneous power: $$p(t) = v(t) i(t) = V_p sin(2\pi f t) I_p sin(2\pi f t + \beta) =$$ $$= V_p I_p sin(2\pi f t) ( sin(2\pi f t)cos(\beta) + cos(2\pi f t)sin(\beta) ) =$$ $$= V_p I_p sin^2(2\pi f t)cos(\beta) + sin(2\pi f t)cos(2\pi f t)sin(\beta) =$$ $$= V_p I_p \frac{1-cos(4\pi f t)}{2} cos(\beta) + \frac{sin(4\pi f t)}{2} sin(\beta) =$$ $$= \frac{1}{2} V_p I_p cos(\beta) - \frac{1}{2}V_p I_p cos(4\pi f t) cos(\beta) + \frac{1}{2}V_p I_p sin(4\pi f t) sin(\beta)$$
This expression contains three terms: the first one is the average active power, the second one is a part of the fluctuating active power and the third part is the instantaneous reactive power. We can summarize the results in this way: $$P = \frac{1}{2} V_p I_p cos(\beta) \ Average \ Active \ Power \ [W]$$ $$Q = \frac{1}{2} V_p I_p sin(\beta) \ Reactive \ Power \ Modulus \ [VAR]$$ $$p(t) = \frac{1}{2} V_p I_p cos(\beta) - \frac{1}{2}V_p I_p cos(4\pi f t) cos(\beta) \ Instantaneous \ Active \ Power$$ $$q(t) = \frac{1}{2}V_p I_p sin(4\pi f t) sin(\beta) \ Instantaneous \ Reactive \ Power$$ Moving to the phasor form, we can define $$S = \frac{1}{2}V \cdot I^* = P + jQ = |S|\angle \beta\ Complex \ Power \ [VA]$$ $$A = |S| = \sqrt{P^2 + Q^2} \ Apparent \ Power \ [VA]$$ Note that the Apparent Power is the modulus of the Complex Power. cos(β) is called power factor.
If the load is known, one can use it to find S: $$S = \frac{1}{2} V \cdot I^* = \frac{1}{2} Z \cdot I \cdot I^* = \frac{1}{2} Z |I|^2$$
An important note
There is no RMS power! Forget about it! Only currents and voltages can be used in their RMS form to simplify calculations, but RMS power has no physical sense!
When you need to calculate the power dissipated in resistive components, use the average power in W; if you need to know the amount of reactive power circulating between a line and a capacitive or inductive load, use, instead, modulus and phase of the reactive power!
Comments
Be polite and respectful in the comments section. In case of doubts, read this before posting.
Posted comments ⮧
Comment section still empty.
INDEX
INFO
STATISTICS
CONTACTS
SHARE






