RMS values

RMS values - also known as quadratic mean - calculated for different type of periodic waveform

cheatsheet

help

Key concepts

The RMS (Root Mean Square) value is a statistical measure of the magnitude of a varying quantity. It is particularly useful in various fields such as electrical engineering, physics, and signal processing to quantify the effective value of an alternating current (AC) or voltage signal. The RMS value provides a measure that corresponds to the equivalent direct current (DC) value that would deliver the same power to a load.

The concept of RMS value can be applied to:

Electrical Engineering: RMS values are used to specify the voltage and current ratings of AC electrical equipment. For example, household electrical outlets are typically rated in terms of RMS voltage.
Signal Processing: In analyzing signals, the RMS value provides a measure of signal power, which is crucial for communication systems and audio engineering.
Physics and Engineering: RMS values help quantify the energy or power in systems with fluctuating quantities, such as vibrations in mechanical systems or thermal fluctuations.

In summary, the RMS value is a crucial metric for understanding and comparing the power or energy content of varying signals, providing a consistent way to quantify these quantities in practical applications.

In the context of an AC signal or supply line, the RMS value of a sinusoidal voltage or current is particularly important because it represents the equivalent DC value that would produce the same heating effect (power dissipation) in a resistive load.

Definition

The RMS value of an arbitrary discrete function is defined as $$U_{RMS} = \sqrt{\frac{1}{n}(x_1^2 + x_2^2 + ... + x_n^2)} = \sqrt{\frac{1}{n}\sum_{i=1}^n x_i^2}$$

The RMS value of an arbitrary continuous function is defined as $$U_{RMS} = \sqrt{\frac{1}{T_2-T_1}\int_{T_1}^{T_2}[f(t)]^2 dt}$$

The RMS value of an arbitrary periodic continuous function is defined as $$U_{RMS} = \sqrt{\frac{1}{T}\int_{0}^{T}[f(t)]^2 dt}$$

Fundamental property

RMS values can be combined with the following properties: $$RMS\{f(t)+g(t)\}=\sqrt{ RMS^2\{f(t)\} + RMS^2\{g(t)\} }$$

RMS values

Waveform	Function	RMS value
Constant	$$f(t) = A, \quad A \in \mathbb{R}$$	$$A$$
Sine wave	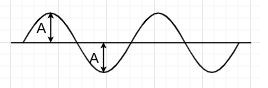$$f(t) = Asin(2 \pi f t), \quad A \in \mathbb{R}$$	$$\frac{A}{\sqrt{2}}$$
Half-Rectified Sine wave	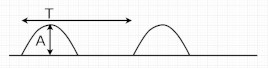$$f(t) = \begin{cases} Asin(2 \pi f t), \quad kT \le t \lt kT+0.5T \\ 0, \quad kT+0.5T \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$\frac{A}{2}$$
Full-Rectified Sine wave	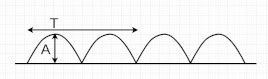$$f(t) = \begin{cases} Asin(2 \pi f t), \quad kT \le t \lt kT+0.5T \\ Asin(2 \pi f t), \quad kT+0.5T \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$\frac{A}{\sqrt{2}}$$
Zero-based square wave	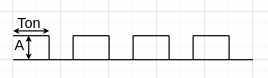$$f(t) = \begin{cases} A, \quad kT \le t \lt kT+T_{on} \\ 0, \quad kT+T_{on} \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$A\sqrt{D}$$
Zero-centered square wave	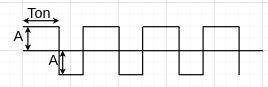$$f(t) = \begin{cases} A, \quad kT \le t \lt kT+T_{on} \\ -A, \quad kT+T_{on} \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$A$$
NonZero-centered square wave	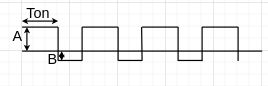$$f(t) = \begin{cases} A, \quad kT \le t \lt kT+T_{on} \\ -B, \quad kT+T_{on} \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$\sqrt{A^2 \cdot D + B^2 \cdot (1-D)}$$
Zero-centered triangle wave	$$f(t) = A\int sign(sin(2\pi ft)), \quad A \in \mathbb{R}$$	$$\frac{A}{\sqrt{3}}$$
Pulsed triangle wave	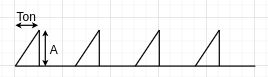$$f(t) = \begin{cases} \frac{A}{T_{on}}t, \quad kT \le t \lt kT+T_{on} \\ 0, \quad kT+T_{on} \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$A\sqrt{\frac{D}{3}}$$
NonZero-based pulsed triangle wave	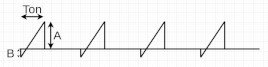$$f(t) = \begin{cases} \frac{A-B}{T_{on}}t+B, \quad kT \le t \lt kT+T_{on} \\ 0, \quad kT+T_{on} \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$\sqrt{\frac{D}{3}(A^2+AB+B^2)}$$
Zero-based trapezoidal wave	$$f(t) = \begin{cases} V_l+\frac{V_h-V_l}{T_{on}}t, \quad kT \le t \lt kT+T_{on} \\ 0, \quad kT+T_{on} \le t \lt (k+1)T \end{cases}, \quad k \in \mathbb{N} $$	$$\sqrt{\frac{D}{3}(V_l^2+V_l V_h + V_h^2)}$$
Exponential wave	$$f(t) = Ae^{\frac{-t}{\tau}}, \quad kT \le t \lt (k+1)T, \quad k \in \mathbb{N} $$	$$A\sqrt{\frac{\tau}{2T}}$$

Constant

$$U_{RMS} = \sqrt{\frac{1}{T}\int_{0}^{T}[A]^2 dt} = $$ $$= \sqrt{\frac{1}{T} A^2 \rvert_0^T} = \sqrt{\frac{1}{T} (A^2 T)} = A$$

Sine wave

$$U_{RMS} = \sqrt{\frac{1}{T}\int_{0}^{T}[Asin(2\pi ft)]^2 dt} = \sqrt{\frac{A^2}{T}\int_{0}^{T}[sin(2\pi ft)]^2 dt} = $$ $$= \sqrt{\frac{A^2}{T} \int_{0}^{T} \frac{1-cos(4\pi ft)}{2} dt} = \sqrt{\frac{A^2}{2T} (t-\frac{sin(4\pi ft)}{4\pi f}) \rvert_0^T } = $$ $$= \sqrt{\frac{A^2}{2T} (T-\frac{sin(4\pi fT)}{4\pi f} - 0)} = \sqrt{\frac{A^2}{2T}T} = \frac{A}{\sqrt{2}}$$

Half-Rectified Sine wave

$$U_{RMS} = \sqrt{\frac{1}{T}\int_{0}^{T}[f(t)]^2 dt} = \sqrt{\frac{1}{T}\int_{0}^{T/2}[Asin(2 \pi f t)]^2 dt} = \sqrt{\frac{1}{T}\int_{0}^{T/2}[A^2\frac{1-cos(4 \pi f t)}{2}] dt} = $$ $$\sqrt{\frac{A^2}{2T} \left( t-\frac{sin(4\pi f t)}{4\pi f}\right) \rvert_{0}^{T/2} } = \sqrt{\frac{A^2}{2T} \frac{T}{2}- 0 - 0 + 0} = \frac{A}{2}$$

Full-Rectified Sine wave

$$U_{RMS} = \sqrt{\frac{1}{T/2}\int_{0}^{T/2}[Asin(2\pi ft)]^2 dt} = \sqrt{\frac{A^2}{T/2}\int_{0}^{T/2}[sin(2\pi ft)]^2 dt} = $$ $$= \sqrt{\frac{A^2}{T/2} \int_{0}^{T/2} \frac{1-cos(4\pi ft)}{2} dt} = \sqrt{\frac{A^2}{T} (t-\frac{sin(4\pi ft)}{4\pi f}) \rvert_0^{T/2} } = $$ $$= \sqrt{\frac{A^2}{T} (T/2-\frac{sin(4\pi fT/2)}{4\pi f} - 0)} = \sqrt{\frac{A^2}{T}T/2} = \frac{A}{\sqrt{2}}$$

Zero-based square wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [Af(t)]^2 dt} = \sqrt{\frac{1}{T} \int_{0}^{T_{on}} [A]^2 dt} = $$ $$= \sqrt{\frac{1}{T} tA^2 \rvert_0^{T_{on}}} = \sqrt{\frac{1}{T} T_{on}A^2 } = A\sqrt{D}$$

Zero-centered square wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [Af(t)]^2 dt} = \sqrt{\frac{1}{T} (\int_{0}^{T_{on}} [A]^2 dt + \int_{T_{on}}^T [-A]^2 dt)} = $$ $$= \sqrt{\frac{1}{T} (tA^2 \rvert_0^{T_{on}} + t(-A)^2 \rvert_{T_{on}}^T) } = \sqrt{\frac{1}{T} (T_{on}+T_{off})A^2 } = A$$

NonZero-centered square wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [f(t)]^2 dt} = \sqrt{\frac{1}{T} (\int_{0}^{T_{on}} [A]^2 dt + \int_{T_{on}}^T [-B]^2 dt)} = $$ $$= \sqrt{\frac{1}{T} (A^2 t\rvert_{0}^{T_{on}} + B^2 t\rvert_{T_{on}}^{T}) } = \sqrt{A^2 \cdot D + B^2 \cdot (1-D)} $$

Zero-centered triangle wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [Af(t)]^2 dt} = $$

Pulsed triangle wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [f(t)]^2 dt} = \sqrt{\frac{1}{T} \int_{0}{T_{on}} (\frac{A}{T_{on}}t)^2 dt} =$$ $$= \sqrt{\frac{1}{T} \frac{A^2}{3T_{on}^2}t^3)^2 \rvert_{0}^{T_{on}} } = A\sqrt{\frac{D}{3}}$$

NonZero-based pulsed triangle wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [f(t)]^2 dt} = \sqrt{\frac{1}{T} \int_{0}{T_{on}} (\frac{A-B}{T_{on}}t + B)^2 dt} =$$ $$= \sqrt{\frac{1}{T} (\frac{A^2-2AB+B^2}{3T_{on}^2}t^3 + \frac{A-B}{T_{on}}Bt^2 + B^2 t) \rvert_{0}^{T_{on}} } = \sqrt{\frac{D}{3}(A^2+AB+B^2)}$$

Zero-based trapezoidal wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [f(t)]^2 dt} = \sqrt{\frac{1}{T} \int_{0}^{T_{on}} (V_l+\frac{V_h-V_l}{T_{on}}t)^2 dt + \int_{T_{on}}^{T} 0^2 dt} = $$ $$= \sqrt{\frac{1}{T} (V_l^2t + V_l\frac{V_h-V_l}{T_{on}}t^2 + \frac{(V_h-V_l)^2}{3T_{on}^2}t^3) \rvert_{0}^{T_{on}}} = \sqrt{\frac{1}{T} (V_l^2T_{on} + V_l\frac{V_h-V_l}{T_{on}}T_{on}^2 + \frac{(V_h-V_l)^2}{3T_{on}^2}T_{on}^3) } = $$ $$= \sqrt{\frac{1}{T} (V_l^2T_{on} + V_lV_hT_{on} - V_l^2T_{on} + \frac{V_h^2+V_l^2-2V_hV_l}{3}T_{on})} = \sqrt{\frac{T_{on}}{3T}(V_h^2 + V_l^2 + V_hV_l)}$$

Exponential wave

$$U_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [f(t)]^2 dt} = \sqrt{\frac{1}{T} \int_{0}^{T} (Ae^{\frac{-t}{\tau}})^2 dt} =$$ $$= \sqrt{\frac{A^2}{T} \int_{0}^{T} e^{\frac{-2t}{\tau}} dt} = \sqrt{ \frac{A^2}{T} \frac{-\tau}{2} e^{\frac{-2t}{\tau}}\rvert_{0}^{T} } = $$ $$= \sqrt{\frac{-\tau A^2}{2T} (e^{\frac{-2T}{\tau}}-1) } \approx A \sqrt{\frac{\tau}{2T}}$$