Transmission lines - Part V: Impedances

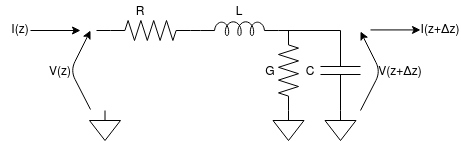
From the telegraphists' equation, two expressions for voltage and current along the transmission line have been found. Now, since Ohm's law is still valid, we can say that voltage and current are related by the following formula. $$Z(z)=\frac{V(z)}{I(z)}$$ But, as you see, we have a spatial dependency of the impedance on the line! Impedance is not constant (as usually is for DC or low frequency circuits), but changes with z variable: $$Z(z) = \frac{V_0^+e^{-jkt}+V_0^-e^{jkt}}{I_0^+e^{-jkt}+I_0^-e^{jkt}}$$ $$Z(z) = \frac{V_0^+(cos(kz)-jsin(kz))+V_0^-(cos(kz)+jsin(kz))}{I_0^+(cos(kz)-jsin(kz))+I_0^-(cos(kz)+jsin(kz))}$$ $$Z(z) = \frac{V_0^+(cos(kz)-jsin(kz))+V_0^-(cos(kz)+jsin(kz))}{Y_{\infty}V_0^+(cos(kz)-jsin(kz))-Y_{\infty}V_0^-(cos(kz)+jsin(kz))}$$ $$Z(z)= Z_{\infty}\frac{(V_0^++V_0^-)cos(kz)-(V_0^+-V_0^-)jsin(kz)}{(V_0^+-V_0^-)cos(kz)-(V_0^++V_0^-)jsin(kz)}$$ $$Z(z)= Z_{\infty}\frac{(V_0^++V_0^-)cos(kz)-Z_{\infty}(I_0^++I_0^-)jsin(kz)}{Z_{\infty}(I_0^++I_0^-)cos(kz)-(V_0^++V_0^-)jsin(kz)}$$ Dividing by cos(kz) and by (I₀⁺+I₀^-) we get a simpler formula: $$Z(z)= \frac{Z(0)-Z_{\infty}jtan(kz)}{1-Z(0)Y_{\infty}jtan(kz)}$$ Z(0) is the impedance at a known point of the transmission line (usually the load). Then, to go back to the generator we have to move backwards on the line by applying the length of the line stub to the tangent argument z.

Actually, using this formula during calculations by hand is not so comfortable so another tool can be used: the so-called Smith chart, explained in the next article.