Oscillators - Part I

It is pretty difficult to make a circuit to oscillate when you want to build an oscillator (and pretty easy to make an oscillator when you don't), so how to make it properly oscillate? How can we ensure that the oscillation will start and will sustain itself with no natural decay? The physicist Heinrich Barkhausen found two necessary but not sufficient conditions for oscillation: the loop gain must be 1 and the phase shift along the loop must be 2π or multiple of it - which means having a positive reaction; if there exists at least one point in our loop function in which these conditions are satisfied then, probably, the system will oscillate. Remember: there exist circuits that satisfy this criterion but do not oscillate!

$$|T(s)| = 1$$ $$arg[T(s)] = 2\pi n, n \in \mathbb{N}^+$$ These conditions can be rewritten as $$T(s_r) = 1 + 0j, \quad s_r \in \mathbb{C}$$ So there must be at least one point (one pulsation value) in which the imaginary part of the loop function is 0 and the real part is 1. Please, note that to generate a sustainable oscillation, one must have a very high gain during the power on: oscillation is permitted only if there is enough noise to be amplified during startup. When the frequency component is met (it is present in a stochastic noise process), it is amplified at the beginning then it reaches the unity gain after the startup ramp ends and sustains itself.

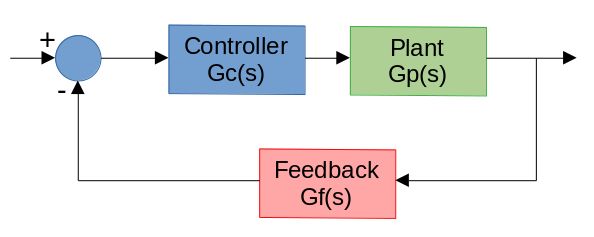
The idea behind an oscillator is to do exactly the opposite of a common closed-loop control system, in which a high gain/high phase margin is desirable at low frequencies, while a low gain/low phase margin is required at higher frequencies to ensure stability: typically one wants to have a very high direct gain so that the close loop control function depends exclusively from the feedback network but, at the same time such gain must be kept low enough to ensure that higher frequencies are attenuated rather than amplified.

To make the system oscillate and to ensure that such oscillation is self-sustaining we can have a gain that is perfectly 1 (in this case we will have a perfect sine wave) or higher than 1 (after some time the output signal of the oscillator will be clamped). If the gain is lower than one we will observe a naturally damped oscillation; that happens in low-phase margin systems, which tend to instability and fast response with an excessive overshoot.

An oscillator, typically, doesn't need a setpoint (except voltage-controlled oscillators) since it should self-sustain and start autonomously but we will see that, instead, it is good to provide a bias point.

Harmonic (or sine wave) oscillators generate ideally perfect sine wave at their outputs. They use the initial gain of an amplifier working in its linear region and then, it will reach the unit gain, self-sustaining the oscillation. After the amplifier, there is a filter that helps to increase the phase shift to 360° (typically the amplifier is in an inverting configuration and the remaining 180° shift is obtained through a double pole filter).

Relaxation oscillators can be seen as sine wave oscillators with a very high gain whose modulus is positive (and, obviously, higher than one), producing thus very steep edges or as non-linear oscillators going back and forth between two admissible states. They are very good oscillators since they are simple, easily tunable, and with a low component count. However, they do not provide a very high accuracy: they typically are temperature, ageing and bias voltage-dependent. Moreover, since the generated wave is a square wave, you'll get a lot of harmonics and so, probably, more EMC issues. Examples of non-linear oscillators are ring oscillators, multivibrators, and delay line oscillators.