➔ Index of ⦁ Oscillators Theory and Circuits ⦁

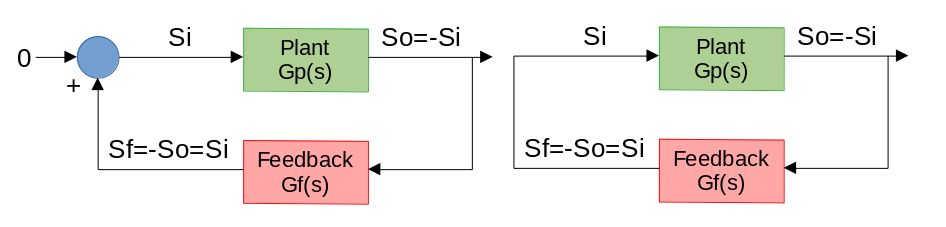
Colpitts oscillator is made of an amplifying stage and a filter that adds a 180° phase shift to the output signal. In this case, let's set capacitor ESR and inductor DCR respectively to 0Ohm and 1mOhm. Moreover, let's assume that the oscillation is not influenced by the used nMOS. It works following a simple principle: when the supply rises, automatically the gate voltage of the transistor is slowly sent to a high voltage; after some time such voltage is high enough to reach the MOS threshold voltage and when this happens, the voltage at the output decreases but, again, when this happens the gate voltage decreases too with some phase shift and this causes the output voltage to rise again. This circuit works without bias point since, during startup, the gate is polarized through the output resistor.

Small signal model

Let's find the loop function T(s). Capacitors ESR and inductor DCR are neglected; neither the nMOS properties are considered, just transconductance. Calculations are shown below, assuming that the device is in its saturation region, with a gate voltage close to the threshold voltage, far away from linearity.

Note that, in the following expressions, C_d is C9 and C_g is C8 $$ V_O = - g_m V_I ( R_O // \frac{1}{sC_d} // (sL+\frac{1}{sC_g}) ) (\frac{\frac{1}{sC_g}}{sL+\frac{1}{sC_g}}) $$

Now let's define $$a = R_O // \frac{1}{sC_d} = \frac{R_O \frac{1}{sC_d}}{R_O + \frac{1}{sC_d}} = \frac{R_O}{sR_OC_d + 1}$$ $$b = (\frac{\frac{1}{sC_g}}{sL+\frac{1}{sC_g}}) = \frac{1}{1+s^2LC_g}$$

Finally, we get the following expression for the open loop transfer function T(s) $$V_O = -g_m V_I \frac{a (sL+\frac{1}{sC_g})}{a + (sL+\frac{1}{sC_g})} b = -g_m V_I \frac{a(s^2LC_g+1)}{s^2LC_g+saC_g+1}b$$ $$V_O = -g_m V_I \frac{R_O}{sR_OC_d + 1} \frac{(s^2LC_g+1)}{s^2LC_g+s \frac{R_O}{sR_OC_d + 1} C_g+1} \frac{1}{1+s^2LC_g}$$ $$V_O = -g_m V_I \frac{R_O}{s^3R_OC_dC_gL + s^2C_gL + sR_OC_g + sR_OC_d + 1}$$ $$T(s) = \frac{-g_mR_O}{s^3R_OC_dC_gL + s^2C_gL + sR_O(C_g+C_d) + 1}$$

Now let's move from the Laplace domain to the frequency domain, where s=jw $$T(j\omega) = \frac{-g_mR_O}{-j\omega ^3 R_OC_dC_gL - \omega^2C_gL + j\omega R_O(C_g+C_d) + 1}$$

In the previous article we saw that the Barkhausen criterion is satisfied if there exists at least one value of w for which T(jw) = 1+j0, so we can find two conditions $$\begin{cases} -j\omega ^3 R_OC_dC_gL + j\omega R_O(C_g+C_d) = 0 \\ \frac{-g_mR_O}{-\omega^2C_gL + 1} = 1 \end{cases}$$ $$\begin{cases} \omega = \sqrt{\frac{C_g+C_d}{C_gC_dL}} \\ g_mR_O = \frac{C_g}{C_d} \end{cases}$$

Simulation

Let's simulate the circuit: we can divide the startup into three different sections.

Startup The circuit receives supply at t=0s; in this moment, gate and drain terminals are at 0V. Drain voltage rises with a tau=R*(C_d+C_g), and the same happens to gate voltage
Gate voltage reaches Vth The gate voltage approaches the threshold voltage and the MOSFET starts conducting. When this happens, the drain voltage decreases while the gate voltage increases because of the energy stored in the inductor. The more the gate voltage increases, the more the MOSFET conducts; the more the gate voltage decreases, the more the gate voltage will decrease with some delay
Stable oscillation The MOSFET is now conducting and the gate voltage is still over the threshold. The gate voltage begins to decrease since the current in the inductor decreases, moving the transistor to its cutoff region; when this happens, the drain voltage rises again, letting the gate voltage rise again. After some repetition of this cycle, the circuit reaches its stable oscillation condition, with a frequency imposed by L and C values