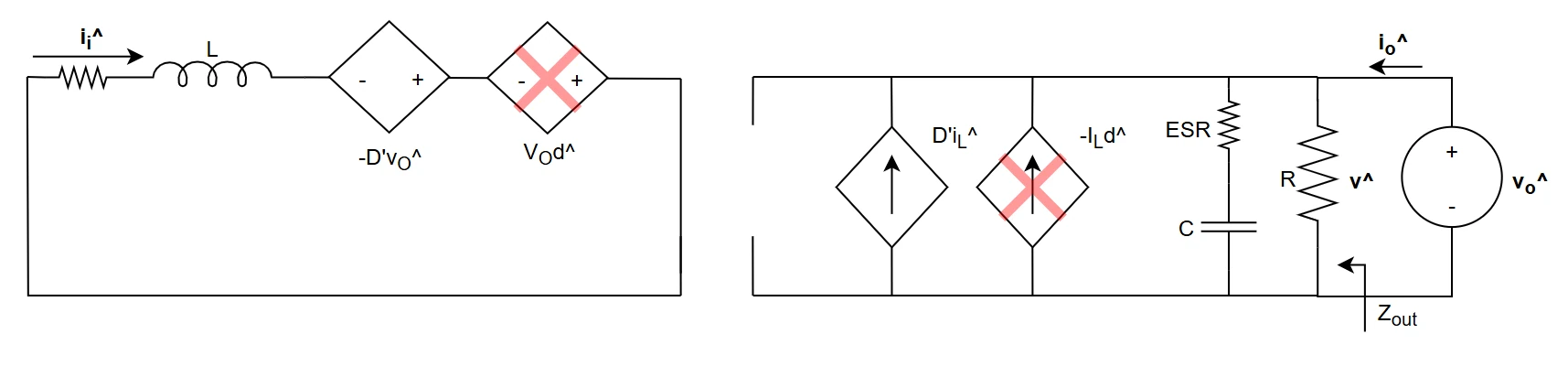
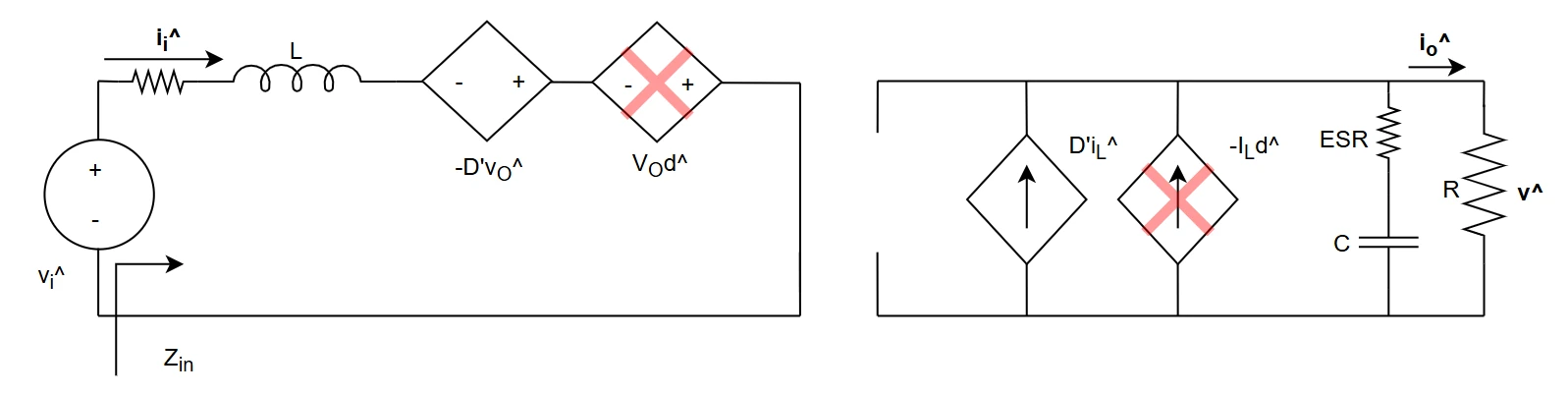
Boost CCM input-output relation
First, let's find the input-output relation of a CCM boost, assuming that the voltage across the inductor has a sum of 0V along the whole switching period. $$\begin{cases} \Delta I_L = \frac{V_I}{L}T_{on} = \frac{V_I}{Lf_{sw}}D\\ \Delta I_L = \frac{V_I-V_O}{L}T_{off} = \frac{V_I-V_O}{Lf_{sw}}D' \end{cases}$$ $$\frac{V_I}{Lf_{sw}}D= -\frac{V_I-V_O}{Lf_{sw}}D' \qquad \rightarrow \qquad D = \frac{V_I-V_O}{V_O}$$
Boost DCM input-output relation
Input-output relation in a boost converter operating in DCM is more complicated than CCM; here are the calculations. D is defined as turn-on time over a period and D' is turn-off time without idle time. $$\begin{cases} \Delta I_L = \frac{V_I}{L}T_{on} = \frac{V_I}{Lf_{sw}}D\\ \Delta I_L = \frac{V_I-V_O}{L}T_{off} = \frac{V_I-V_O}{Lf_{sw}}D' \end{cases} \qquad \rightarrow \qquad \begin{cases} T_{off} = \frac{V_I}{V_O-V_I}T_{on}\\ I_{L,avg} = \frac{T_{on}+T_{off}}{2T}I_{L,pk} = \frac{V_O(T_{on}+T_{off})}{R T_{off}}\\ I_{L,pk} = \frac{V_I}{L}T_{on} \end{cases}$$ $$\begin{cases} T_{off} = \frac{V_I}{V_O-V_I}T_{on}\\ \frac{T_{on}+\frac{V_I}{V_O-V_I}T_{on}}{2T}\frac{V_I}{L}T_{on} = \frac{V_O(T_{on}+\frac{V_I}{V_O-V_I}T_{on})}{R \frac{V_I}{V_O-V_I}T_{on}}\\ I_{L,pk} = \frac{V_I}{L}T_{on} \end{cases} \qquad \rightarrow \qquad \begin{cases} T_{off} = \frac{V_I}{V_O-V_I}T_{on}\\ \frac{T_{on}+\frac{V_I}{V_O-V_I}T_{on}}{2T}\frac{V_I}{L}T_{on} = \frac{V_O(T_{on}+\frac{V_I}{V_O-V_I}T_{on})}{R \frac{V_I}{V_O-V_I}T_{on}}\\ I_{L,pk} = \frac{V_I}{L}T_{on} \end{cases}$$ $$\begin{cases} T_{off} = \frac{V_I-V_O}{V_O}T_{on}\\ V_O^2 - V_I V_O - \frac{RV_I^2 D^2}{2Lf_{sw}} = 0 \\ I_{L,pk} = \frac{V_I-V_O}{L}T_{on} \end{cases} \qquad \rightarrow \qquad V_O = \frac{V_I+\sqrt{V_I^2+4*\frac{RV_I^2 D^2}{2Lf_{sw}}}}{2} $$
Boost CCM and DCM - Critical inductance
Like for the buck, also the boost converter has a critical inductance that is the minimum required to ensure that our DCDC will operate in CCM. $$\begin{cases} \Delta I_L = \frac{V_I}{L}T_{on} = \frac{V_I}{Lf_{sw}}D\\ \Delta I_L = \frac{V_I-V_O}{L}T_{off} = \frac{V_I-V_O}{Lf_{sw}}D' \end{cases}$$ Now we can find the critical inductance whose value sets the boost to work in BCM (Boundary mode), coming from CCM (so calculations are done considering CCM input-output relation) $$\overline{i_L} - \frac{\Delta I_L}{2} = 0$$ $$\frac{V_O}{RD'} - \frac{V_ID}{2Lf_{sw}} = 0$$ Rearranging the terms, we can obtain $$L = \frac{R D' V_I D}{2 V_O f_{sw}} = \frac{R D'^2 D}{2 f_{sw}} $$
Comments
Be polite and respectful in the comments section. In case of doubts, read this before posting.
Posted comments ⮧
Comment section still empty.
INDEX
INFO
STATISTICS
NEXT ARTICLE
CONTACTS
SHARE