General Feedback Theorem

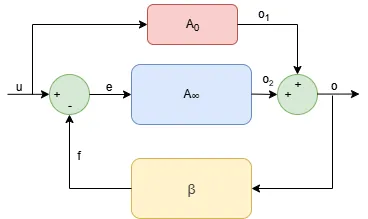
Middlebrook’s General Feedback Theory (GFT) is a powerful tool because it highlights the significance of direct coupling between input and output in feedback systems. This direct path (very often overlooked in traditional loop analysis) can dominate system behavior, particularly in high-performance analog circuits. GFT allows engineers to isolate and quantify this coupling, revealing how it shapes gain, bandwidth, and stability. By focusing on signal flow rather than just topology, GFT delivers low-entropy, design-relevant insights that make it easier to optimize circuits with precision and clarity.

The Middlebrook's General Feedback Theorem formula is $$G(s) = \frac{u_o}{u_i} = G_{\infty}\frac{T}{1+T} + G_0\frac{1}{1+T}$$ where $$T(s) = \frac{u_y}{u_x} \rvert_{u_i=0} \qquad T_n(s) = \frac{u_y}{u_x} \rvert_{u_0\rightarrow 0}$$ $$G_{\infty}(s) = \frac{u_o}{u_i} \rvert_{u_y\rightarrow 0} \qquad G_{0}(s) = \frac{u_o}{u_i} \rvert_{u_x\rightarrow 0}$$ and here is the reprocity relationship $$\frac{T_n(s)}{T(s)} = \frac{G_{\infty}(s)}{G_0(s)}$$