➔ Index of ⦁ Buck Converter ⦁
Buck converter - Input impedance
Open loop input impedance of a buck converter
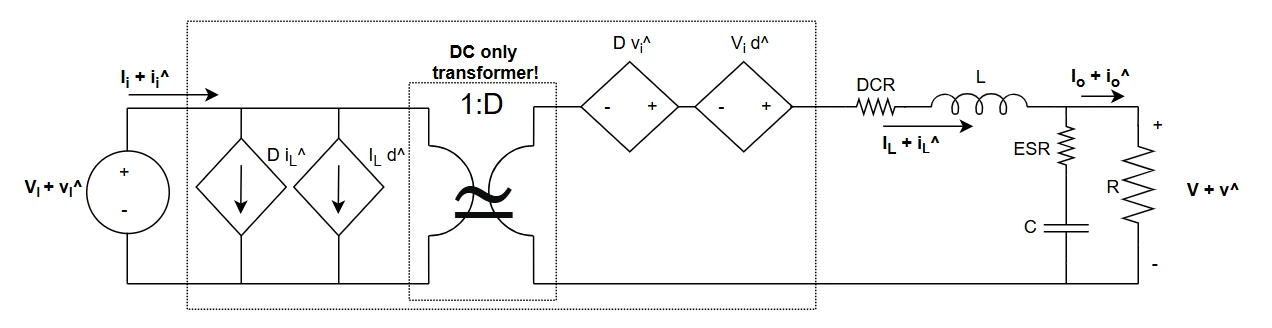
Power stage input impedance
Now, let's find the open loop input impedance of the power stage. The scheme to be used is the following one: the DC transformer is removed and the d^ source is nulled.
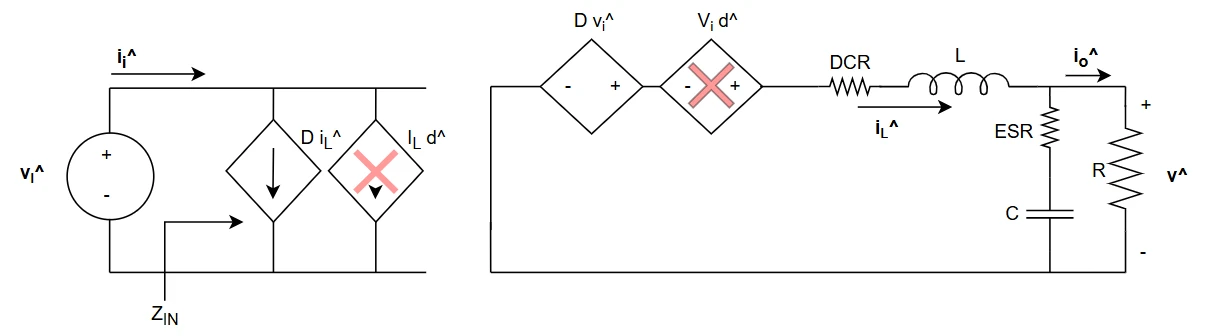
We know that $$ \hat i_{in} = D \hat i_L + \hat d I_L$$ but the dependency from d^ is nulled. Using the power stage functions found in previous articles, and substituting one in another we can find that $$ Z_{in,OL} = \frac{\hat v_{i}}{\hat i_{i}} = \frac{R}{D^2} \frac{s^2 + s\frac{L}{R} + 1}{sCR+1}$$ in DC (s=0) the open loop input impedance becomes $$ Z_{in,OL} = \frac{R}{D^2} $$ and this result can be obtained in this simple way, using the DC model of the buck converter $$\begin{cases} V_O = D V_I \\ I_O = \frac{V_O}{R} \\ P_O = P_I \ \rightarrow \ V_O I_O = V_I I_I \end{cases}$$ Substituting the to leaving just VI and II in the formula, the same result appear.
Comments
Be polite and respectful in the comments section. In case of doubts, read this before posting.
Posted comments ⮧
Comment section still empty.
INDEX
INFO
STATISTICS
PREVIOUS ARTICLE
NEXT ARTICLE
CONTACTS
SHARE