Buck converter - Output impedance

Now, let's find the open loop output impedance of the power stage. This parameter is very important because it helps to calculate the output response in case the load current changes.

The scheme to be used is the following one: the DC transformer is removed, as well as d^ and v_i^ sources that are both nulled. Di_L^, on the input side, instead is not removed since i_L^ is not zero.

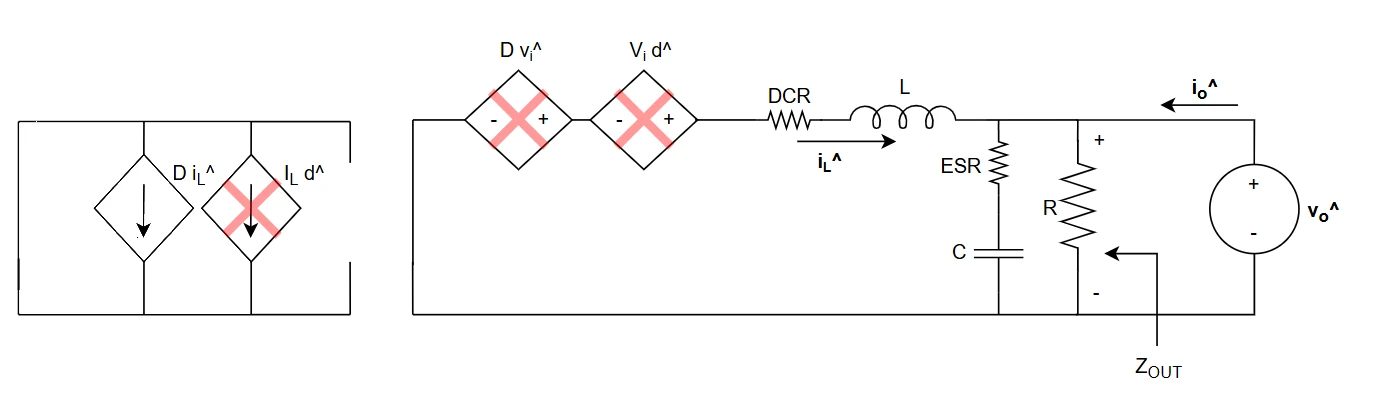
Output impedance is useful to determine if the filtering at the output is enough, the output impedance of the buck converter is low enough to ensure proper behaviour of other supplies, guarantee stability and so on. Output impedance, in case of open loop power stage, is defined as $$ Z_{out,OL} = \frac{\hat v_o}{\hat i_o}$$ In the small signal model, all the other first order sources are set to 0, so it's easy to see that $$ Z_{out,OL} = R//\frac{1}{sC}//sL = \frac{sL}{s^2 LC + s\frac{L}{R} + 1} $$

The ESR of the output capacitor must be always considered when analysing the output impedance of a DCDC converter, as it's very important for stability. The open loop output impedance expression becomes $$Z_{out,OL} = R//(ESR+\frac{1}{sC})//sL = \frac{sL(sC \cdot ESR + 1)}{s^2 LC (1+\frac{ESR}{R}) + s(\frac{L}{R} + C \cdot ESR) + 1}$$

The DCR is used to model the RDSon of the MOSFET and the inductor series resistances. This parameters is very often neglected. $$Z_{out,OL} = R//(ESR+\frac{1}{sC})//(sL+DCR) = \frac{R \cdot DCR}{R+DCR}\frac{(s\frac{L}{DCR}+1)(sC \cdot ESR + 1)}{s^2 LC \frac{R + ESR}{R + DCR} + s(\frac{L+C(R+ESR)DCR+R \cdot C \cdot ESR}{R+DCR}) + 1}$$