Transmission lines - Part III: Reflection coefficient

From the solution of the telegraphists' equations it is possible to define the main features of the transmission line, collected below.

$$ \frac{V_{0}^+}{I_{0}^+} = \sqrt{\frac{L}{C}} = Z_0 [Ohm] $$

$$ k = \omega \sqrt{LC} \left[\frac{rad}{m}\right] $$

$$ v_f = \frac{1}{\sqrt{LC}} \left[\frac{m}{s}\right] $$

$$ \lambda = \frac{v_f}{f} = \frac{2 \pi}{k} [m] $$

$$ v_g = \frac{d\omega}{dk} \left[\frac{m}{s}\right] $$

As you can see, the previous equations are composed of two components: a positive wave and a negative one (forward and backward travelling waves): only the real part makes sense from a physical point of view, so the imaginary one can be discarded. Moreover, in these formulas, the frequency of voltage and current signals is not considered, so, it can be added now to introduce the time dependency too, and not only the space one. An additional phase is added to include a residual phase in the V₀ component.

$$ \begin{cases} V^+(z,t) = \Bbb{Re}\{V(z)e^{j\omega t}\}=|V_0^+|cos(\omega t -kz+\phi) \\ I^+(z,t) = \Bbb{Re}\{I(z)e^{j\omega t}\}=|I_0^+|cos(\omega t -kz+\phi) \end{cases} $$

$$ \begin{cases} V^-(z,t) = \Bbb{Re}\{V(z)e^{j\omega t}\}=|V_0^-|cos(\omega t +kz+\phi) \\ I^-(z,t) = \Bbb{Re}\{I(z)e^{j\omega t}\}=|I_0^-|cos(\omega t +kz+\phi) \end{cases} $$

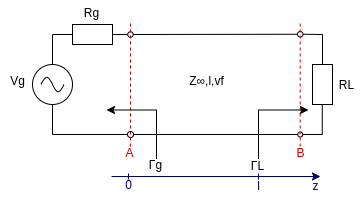
Travelling waves are actual voltage and current waves travelling in two opposite directions in the transmission line. They came out from the mathematical resolution of the telegraphists' equations but which is their physical sense considering that the voltage (or current) signal is applied only at one end of the channel?

When applying a voltage to the input of a transmission line, such voltage propagates to the other end of the line in a finite time and, eventually, is absorbed, partially or totally reflected. Such reflection happens when the characteristic impedance of the line (channel) is different from the impedance of the load (receiver), causing a portion of the voltage to go back and forth in the line and disturbing thus the communication. From this definition, it is possible to define a very important parameter of every transmission line: the reflection coefficient. $$ \Gamma = \frac{V^-(z)}{V^+(z)} = \frac{V_0^-(z)e^{jkz}}{V_0^+(z)e^{-jkz}} = \frac{V_0^-}{V_0^+}e^{2jkz} = \Gamma_0 e^{2jkz}$$

The reflection coefficient is defined as follows at the end of the transmission line, where the load impedance is known: $$V(L,t)=Z_LI(L,t) \to V^+(L,t)+V^-(L,t)=Z_L(I^+(L,t)+I^-(L,t))$$ $$V^+(L,t)+V^-(L,t)=Z_LY_0(V^+(L,t)-V^-(L,t))$$ $$\Gamma_L = \frac{V^-(L)}{V^+(L)} = \frac{Z_L-Z_0}{Z_L+Z_0}$$ In a more general way, we can write $$\Gamma(z) = \frac{V^-(z)}{V^+(z)} = \frac{Z(z)-Z_0}{Z(z)+Z_0}$$ so, the reflection coefficient changes along the line according to the line impedance Z(z) at that point. In the next articles, you'll learn how to calculate or estimate the line impedance along a section of the transmission line.

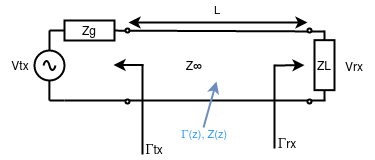
In the image above you see a very simple point-to-point transmission line with the main properties shown. To fully understand what happens at each end, due to the difference between the termination impedances (Z_g and Z_L) and the characteristic impedances (and so due to a reflection coefficient different from 0), it is convenient to shift to the time domain for a while, as explained in the next article.