Boost converter - Output impedance

Now, let's find the open loop output impedance of the power stage. This parameter is very important because it helps to calculate the output response in case the load current changes.

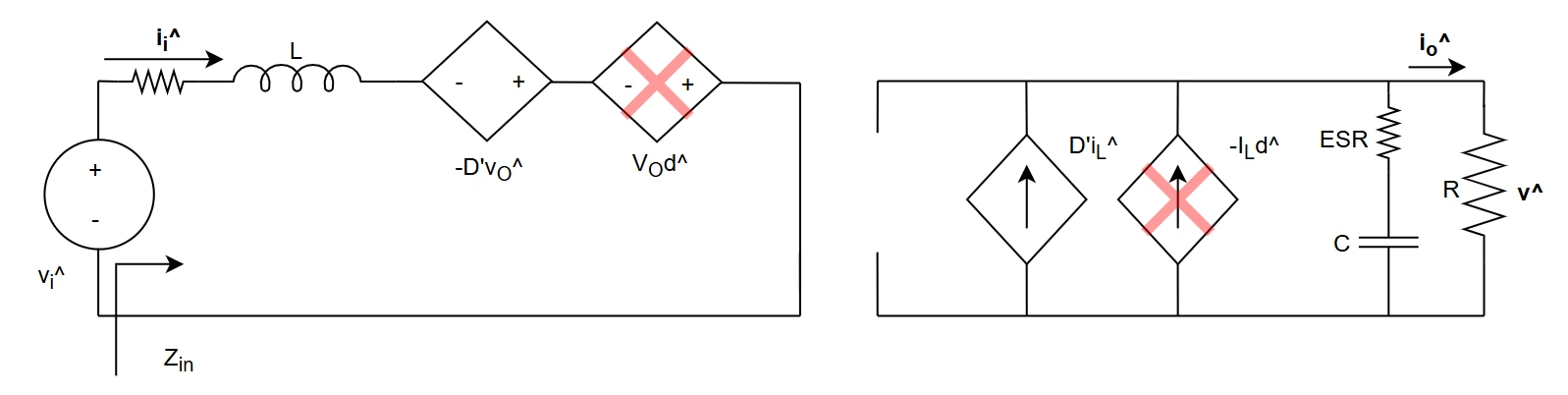
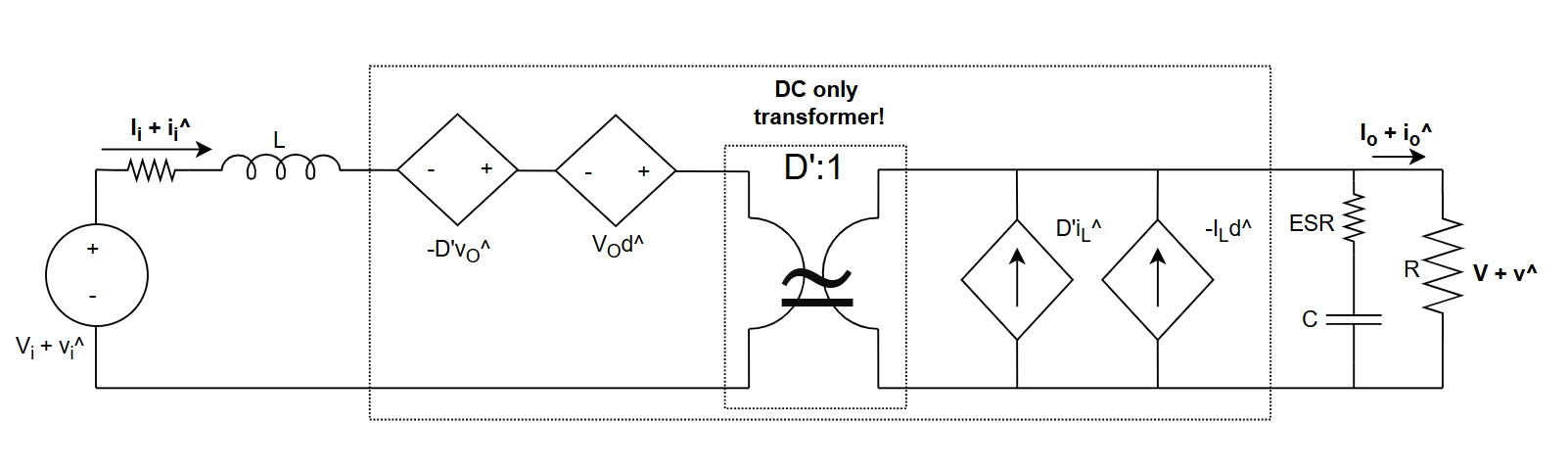
The scheme to be used is the following one: the DC transformer is removed, as well as d^ and v_i^ sources that are both nulled. -Dv_o^, on the input side, instead is not removed since v_o^ is not zero (that's exactly the test voltage applied at the output of the converter). Note that the scheme for output impedance calculation is exactly the same as the one used for input impedance calculation with test voltage source placed at the output.

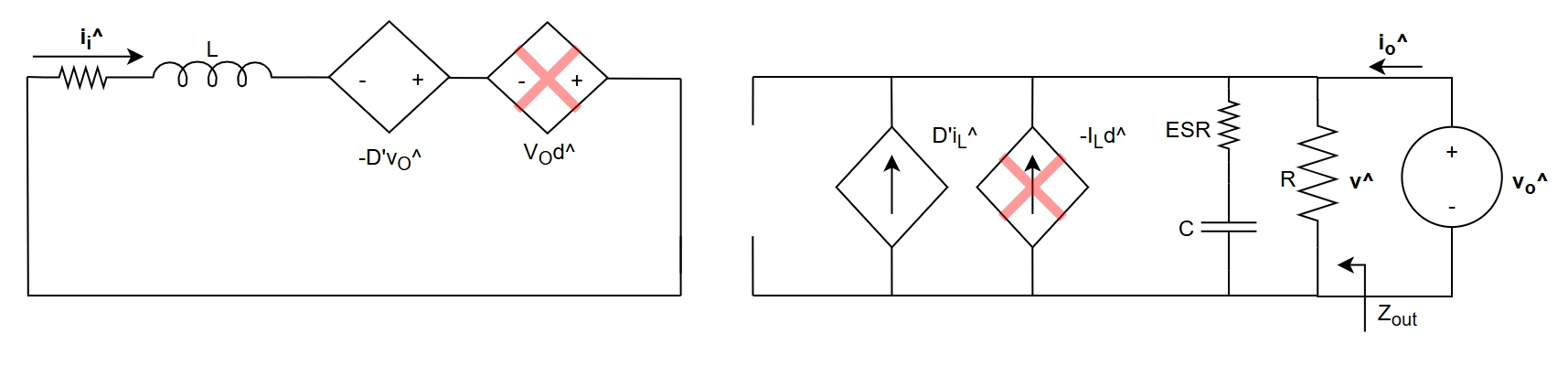
Output impedance is useful to determine if the output impedance of the buck converter is low enough to ensure proper behaviour of other supplies, guarantee stability and so on. Output impedance, in case of open loop power stage, is defined as $$ Z_{out,OL} = \frac{\hat v_o}{\hat i_o}$$ $$\hat v_o = (\hat i_o + D'\hat i_L) \frac{R}{sCR+1} \qquad \hat i_L = \frac{-D'\hat v_o}{sL}$$ $$\hat v_o = (\hat i_o + D'\frac{-D'\hat v_o}{sL}) \frac{R}{sCR+1}$$ $$\hat v_o (1+\frac{D'^2}{sL} \frac{R}{sCR+1}) = \hat i_o \frac{R}{sCR+1}$$ The final result is $$ Z_{out,OL} = \frac{1}{D'^2} \frac{sL}{s^2 \frac{LC}{D'^2} + s\frac{L}{RD'^2} + 1} $$

The ESR of the output capacitor must be always considered when analysing the output impedance of a DCDC converter, as it's very important for stability. The open loop output impedance expression becomes $$Z_{out,OL} = $$

The DCR is used to model the RDSon of the MOSFET and the inductor series resistances. This parameters is very often neglected. $$Z_{out,OL} = $$