➔ Index of ⦁ Transmission Lines Theory ⦁
Transmission lines - Part VIII: T and VSWR
What are T and VSWR and why they are so important
T definition
T is the so-called transmission coefficient of the line. It is dependent on the load impedance and the line matching level. This coefficient allows us to find the overall voltage at an arbitrary section of the TL, knowing only the forward travelling wave. It is defined as $$T(z) = 1+\Gamma(z)$$ It is derived from the following chain of calculations $$V(z) = V^+(z) + V^-(z) = V^+(z)(1+\Gamma(z)) = V^+(z) T(z)$$ If the load is matched to the line impedance T(z)=1; in all the other cases, T(z) is a periodic function.
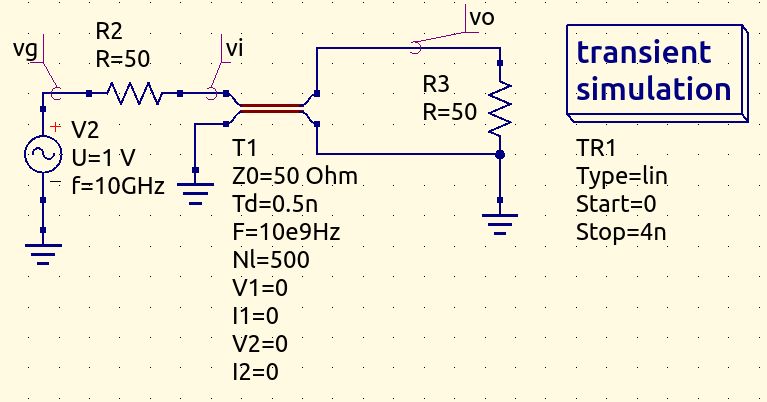
In the following examples the used input data are $$f = 10GHz \qquad v_p = 2\cdot 10^8 m/s \qquad l=0.1m$$
Matched impedance
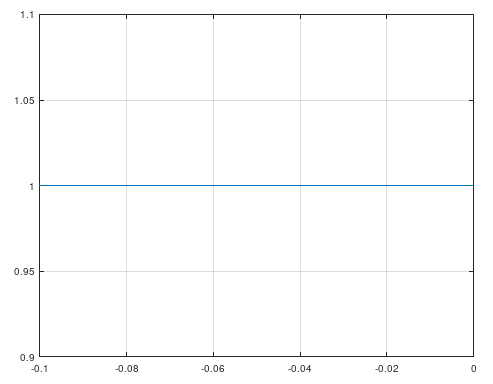
In this case, the transmission coefficient is a constant 1 for the whole length of the line. The voltage at the input (section -0.1m) is the same as the output (section 0m), since k is a multiple of 2pi.
Open circuit
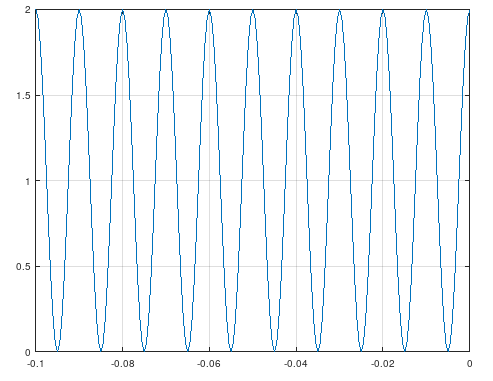
In this case, the voltage at the output (0m) is two times the voltage at the generator. The voltage along the line will have nodes (fixed 0V) and antinodes (oscillating voltage between 0 and the maximum): we have a stationary wave along the line with.
Short circuit
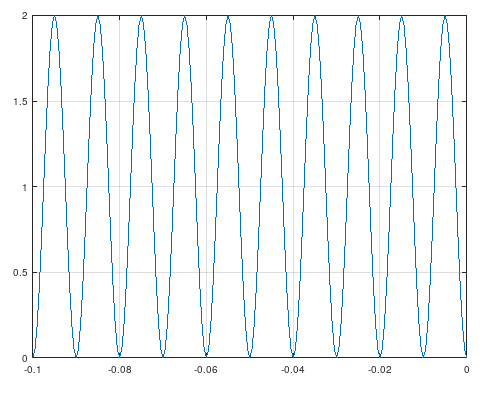
This case is similar to the previous one since we have fixed nodes and antinodes; however, the voltage at the output 0m is always 0V.
VSWR definition
VSWR (Voltage Wave Standing Ratio) is the ratio between the maximum and the minimum voltage that can be found along a transmission line where a standing wave is present. This value is between 1 and infinite; if it's close to 1, then the line is close to perfect impedance matching.
VSWR is defined as $$VSWR = \frac{V_{max}}{V_{min}} = \frac{1+|\Gamma|}{1-|\Gamma|}$$
Navigate
Comments
Be polite and respectful in the comments section. In case of doubts, read this before posting.
Posted comments ⮧
Comment section still empty.
INDEX
INFO
STATISTICS
PREVIOUS ARTICLE
NEXT ARTICLE
CONTACTS
SHARE