Control Theory - LTI and Feedback

Dynamic systems can have many interesting properties but many of them exhibit a certain level of self-regulation, ensuring that the output will always follow a defined profile and be confined between an upper and a lower bounds, even when some external conditions change. This is obtained through negative feedback, a special solution that gives the system the capability .

Negative feedback is obtained though a feedback path from output to input and a comparator; if the error (difference between a reference input and the feedback signal) is positive, then the command sent to the system is positive and negative if the result is negative. The error is actually sent to a controller that elaborates the appropriate stimulus for a given error signal and generates a command to the plant (the part of the system to be controlled).

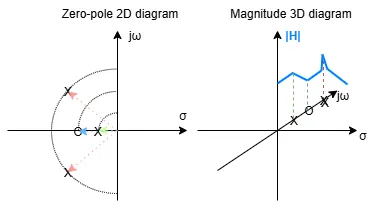
The most common systems are LTI (Linear Time Invariant) and they are designed to be BIBO (Bounded Input Bounded Output) stable. If the system is not linear, then it must be linearized around the working point.

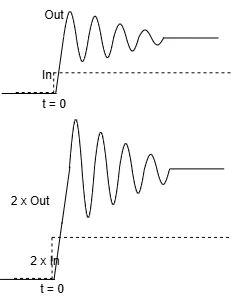
A dynamic system is said to be linear when the output is linearly dependent on the input: doubling the input makes the output to double, halving the input makes the output to halve and so on. If there is another law that regulates input and output, then the system is not linear; it can be quadratic, cubic exponential, it can follow any other profile. In these cases, before analysing the system, we have to find a working point (or bias point) and linearise the system (which consists in linearising the formulas) around it; only at that point we can proceed with the analysis shown in this course.

A linear system follow the rule $$Out = \alpha Out1 + \beta Out2 = \alpha \cdot In1 \cdot H1 + \beta \cdot In2 \cdot H2$$ where H is the so-called transfer function.

Please note that not all system can be easily linearised; when this happens, adaptive control strategies, that are capable of varying parameters and control schemes with working conditions, must be used.

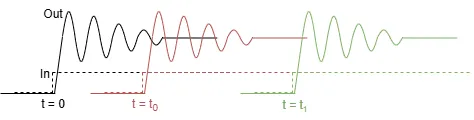
A dynamic system is said to be time-invariant when, if the input is delayed of an arbitrary amount of time t₀, then the output is delayed of the same quantity. The response of the system is always the same, independently on the time.

$$Out(t) = In(t) *\cdot H \rightarrow Out(t-t_0) = In(t-t_0) \cdot H$$ Out(t) has the exact same shape as Out(t-t_0) so the system has no memory of the past; from a mathematical point of view, this means that in the transfer function, 't' is only as an independent variable.

To understand the main components in a simple SISO (Single Input Single Output) feedback LTI system, let's sketch a diagram. You can find the feedback path, the comparator (a subtractor), the direct path (it describes both the controller and the plant).

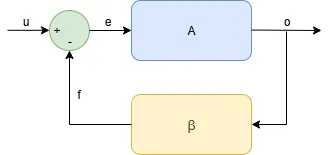
Let's write down the equations: $$\begin{cases} e = u-f \\ o = A \cdot e \\ f = o \cdot \beta \end{cases}$$ Let's do the substitutions $$o = A \cdot (u-o \cdot \beta)$$ $$o = u \cdot \frac{A}{1+A \cdot \beta}$$ A generic negative feedback system is governed by the following transfer function $$H = \frac{o}{u} = \frac{A}{1+A \cdot \beta} = \frac{A}{1+T}$$

From the formula above you can see that it would be desirable to have A very big. In this way the closed-loop function H is mainly dependent on the feedback path, which is the part of the system we design and accurately know. $$H = \frac{o}{u} \sim \frac{1}{\beta}$$ Moreover, from the expression, it's easy to see that H doesn't exist for a denominator equal to 0, which means $$1+A \beta = 0 \quad , \quad A \beta = -1$$ T is called loop function or open-loop function. H is called closed loop function. Many properties of the dynamic system can be analysed and understood studying the open-loop function only.

In many feedback systems, there is a terms that is typically neglected. However, in some occasions, the designer must keep in mind that there is a forward path from the control input to the output.

Let's think about a very simple feedback circuit: the common emitter amplifier topology based on a BJT. the control signal is connected to the base and the output signal is taken at the collector. The emitter resistor act as a feedback: the higher the input signal, the higher the emitter current but the higher the emitter current, the lower the B-E voltage and so the lower the emitter current. This is the normal negative feedback loop, but now, let's look closer to the BJT: there is a parasitic capacitor between base and collector! This is a direct path between input and output, negligible in DC and at low frequency but disruptive at high frequency.

There is a fundamental theorem that helps us to consider this term: the General Feedback Theorem (GFT), developed by Robert D. Middlebrook. Take a look the image below and write down the equations.

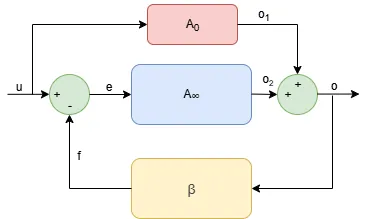
$$\begin{cases} e = u-f \\ o_1 = A_0 \cdot u \\ o_2 = A_\infty \cdot e \\ o = o_1 + o_2 \\ f = (o_1+o_2) \cdot \beta \end{cases}$$ Let's do the substitutions $$o = A_0 \cdot u + A_\infty \cdot e$$ $$o = A_0 \cdot u + A_\infty \cdot (u-o \cdot \beta)$$ $$o = u \cdot \frac{A_0}{1+A_\infty \cdot \beta} + u \cdot \frac{A_\infty}{1+A_\infty \cdot \beta}$$ A generic negative feedback system described by the GFT is governed by the following transfer function $$H = \frac{o}{u} = \frac{A_0}{1+A_\infty \cdot \beta} + \frac{A_\infty}{1+A_\infty \cdot \beta}$$ The closed-loop function is a made of two terms: the first one represents the direct path from input to output and is typically very low (A₀ is low and A_inf is very high) while the other term, which is the typical closed-loop response is often approximated to 1/beta. However this contribution should be considered for some specific systems or frequencies.